小升初数学常考经典几何题目

1、图中的长方形的长与宽的比为8:3，求阴影部分的面积。

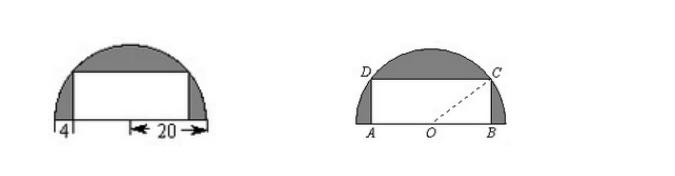
【解】如下图，设半圆的圆心为O，连接OC。

从图中可以看出，OC=20，OB=20-4=16，根据勾股定理可得BC=12。

阴影部分面积等于半圆的面积减去长方形的面积，

为π×202×1/2-（16×2）×12=200π-384=244

2、求下图中阴影部分的面积：

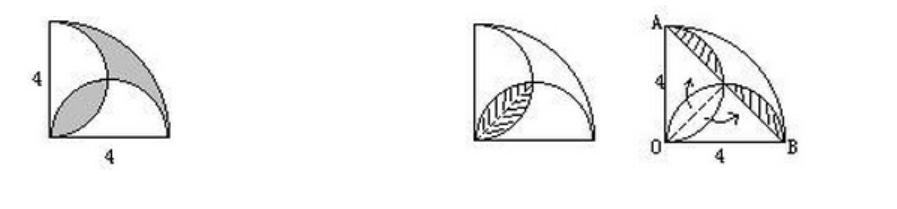
【解】如左上图所示，将左下角的阴影部分分为两部分，然后按照右上图所示，将这两部分分别拼补在阴影位置。可以看出，原题图的阴影部分等于右下图中AB弧所形成的弓形，其面积等于扇形OAB与三角形OAB的面积之差。

所以阴影面积：π×4×4÷4-4×4÷2=4.56

3、如图四边形土地的总面积是48平方米，三条线把它分成了4个小三角形，其中2个小三角形的面积分别是7平方米和9平方米，那么最大的一个三角形的面积是________平方米。

【解】剩下两个三角形的面积和是48-7-9=32，是右侧两个三角形面积和的2倍，故左侧三角形面积是右侧对应三角形面积的2倍，最大三角形面积是9×2=18。

4、已知四边形ABCD和CEFG都是正方形，且正方形ABCD的边长为10厘米，那么图中阴影三角形BFD的面积为多少平方厘米？

【解】连接FC，有FC平行于DB，则四边形BCFD为梯形。

有△DFB、△DBC共底DB，等高，所以这两个三角形的面积相等，显然，△DBC的面积为10×10÷2=50（平方厘米），即阴影部分△DFB的面积为50平方厘米。

5、用棱长是1厘米的正方块拼成如下图所示的立体图形，问该图形的表面积是多少平方厘米？

【解】不管叠多高，上下两面的表面积总是3×3；再看上下左右四个面，都是2×3+1，所以总计9×2+7×4=18+28=46。

6、如图，在△ABC中，AD是AC的三分之一，AE是AB的四分之一，若△AED的面积是2平方厘米，那么△ABC的面积是多少？

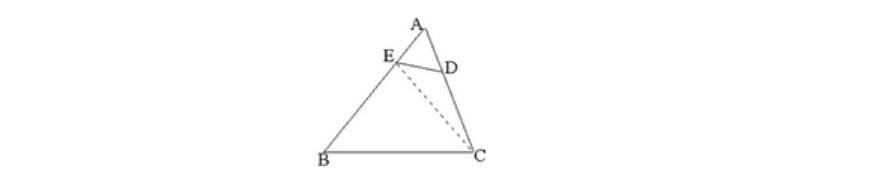
【解】连接EC，如图，因为AC=3AD，△AED与△AEC中AD、AC边上的高相同，所以△AEC的面积是△AED面积的3倍，即△AEC的面积是6平方厘米，用同样方法可判断△ABC的面积是△AEC面积的4倍，所以△ABC的面积是6×4=24（平方厘米）。

7、将三角形ABC的BA边延长1倍到D，CB边延长2倍到E，AC边延长3倍到F，如果三角形ABC的面积等于1，那么三角形DEF的面积是多少？

【解】如图，连接CD、BF，则

△ADC的面积=△ABC的面积=1

△BDE的面积=△BCD的面积×2=（1+1）×2=4

△CDF的面积=△ADC的面积×3=3

△BCF的面积=△ABC的面积×3=3

△BEF的面积=△BCF的面积×2=6

△DEF的面积=△ABC的面积+△ADC的面积+△BDE的面积+△CDF的面积+△BCF的面积+△BEF的面积=1+1+4+3+3+6=18。